Physics-informed neural networks for gravity field modeling of the Earth and Moon
Abstract
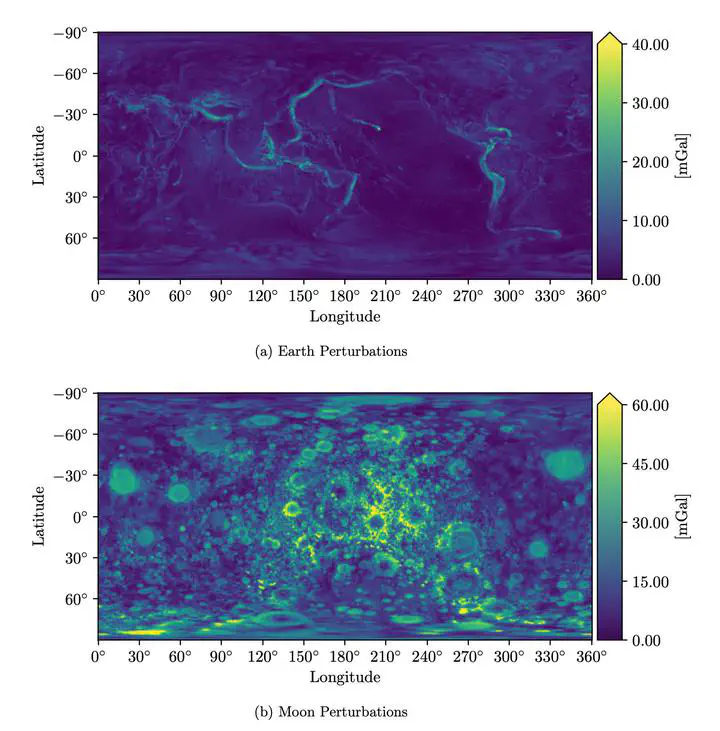
High-fidelity representations of the gravity field underlie all applications in astrodynamics. Traditionally these gravity models are constructed analytically through a potential function represented in spherical harmonics, mascons, or polyhedrons. Such representations are often convenient for theory, but they come with unique disadvantages in application. Broadly speaking, analytic gravity models are often not compact, requiring thousands or millions of parameters to adequately model high-order features in the environment. In some cases these analytic models can also be operationally limiting—diverging near the surface of a body or requiring assumptions about its mass distribution or density profile. Moreover, these representations can be expensive to regress, requiring large amounts of carefully distributed data which may not be readily available in new environments. To combat these challenges, this paper aims to shift the discussion of gravity field modeling away from purely analytic formulations and toward machine learning representations. Within the past decade there have been substantial advances in the field of deep learning which help bypass some of the limitations inherent to the existing analytic gravity models. Specifically, this paper investigates the use of physics-informed neural networks (PINNs) to represent the gravitational potential of two planetary bodies—the Earth and Moon. PINNs combine the flexibility of deep learn- ing models with centuries of analytic insight to learn new basis functions that are uniquely suited to represent these complex environments. The results show that the learned basis set generated by the PINN gravity model can offer advantages over its analytic counterparts in model compactness and computational efficiency.